Subseção 3.1.1 Valor Numérico da Função
Nesta seção vamos usar as funções quadráticas para determinar valores numéricos da função que receberão nomes específicos no estudo de parábolas e que futuramente serão importantes para a resolução de problemas.
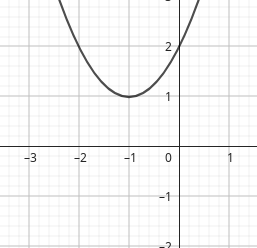
Utilizando a lei de formação \(f(x)=(x+1)^2-4\text{,}\) vamos encontrar alguns pontos específicos. Para isto, faremos o cálculo do valor numérico para os valores inteiros de x pertencentes ao intervalo \([-4,2]\text{.}\) Logo,
\begin{equation*}
f(-4)=(-4+1)^2-4=9-4=5
\end{equation*}
Assim, para um valor de \(x=-4\) temos \(y=5\text{.}\) Veja outros valores:
\begin{align*}
f(-3) \amp =(-3+1)^2-4=4-4=0\\
f(-2) \amp =(-2+1)^2-4=1-4=-3\\
f(-1) \amp =(-1+1)^2-4=0-4=-4\\
f(0) \amp =(0+1)^2-4=1-4=-3\\
f(1) \amp =(1+1)^2-4=4-4=0\\
f(2) \amp =(2+1)^2-4=9-4=5
\end{align*}
Note que temos algumas coincidências que podem ser explicadas pelo eixo de simetria da parábola que é \(x=1\text{,}\) cujos valores distintos de x que estão à mesma distância do eixo de simetria, quando substituidos na fórmula da função, têm como resultado um y de mesmo valor. São os casos de \(f(-4)=f(2)=5\text{,}\) \(f(-3)=f(1)=0\text{,}\) \(f(-2)=f(0)=-3\) e o vértice da função \((-1,-4)\text{.}\)
Portanto, dada a coordenada um x de um ponto, temos o valor numérico de y substituindo x na fórmula da função quadrática. Assim, para a função quadrática do exemplo acima, \(P=(x, (x+1)^2-4)=(x,f(x))=(x,y)\text{.}\)
Acompanhe a seguir outros exemplos e atividades:
Exemplo 3.1.
Observaremos agora um outro exemplo, agora com uma função quadrática na forma padrão \(f(x)=-x^2+6x\text{.}\) Calcularemos \(f(x)\) para \(x\in\{-4,-3,-2,-1,0,1,2,3,4,5\}\text{.}\) Mas antes, vamos escrever a função na forma canônica.
\begin{equation*}
f(x)=a(x-m)^2+k=(-1)\cdot \left(x-\dfrac{-6}{2\cdot(-1)}\right)^2+\dfrac{4\cdot (-1)\cdot(0) -6^2}{4\cdot(-1)}
\end{equation*}
\begin{equation*}
=-(x-3)^2+9
\end{equation*}
Logo, temos que \(f(x)=-(x-3)^2+9\text{.}\) Assim:
\begin{align*}
f(-3) \amp =-(-3-3)^2+9=-36+9=-27\\
f(-2) \amp =-(-2-3)^2+9=-25+9=-16\\
f(-1) \amp =-(-1-3)^2+9=-16+9=-7\\
f(0) \amp =-(0-3)^2+9=-9+9=0\\
f(1) \amp =-(1-3)^2+9=-4+9=5\\
f(2) \amp =-(2-3)^2+9=-1+9=8\\
f(3) \amp =-(3-3)^2+9=0+9=9\\
f(4) \amp =-(4-3)^2+9=-1+9=8\\
f(5) \amp =-(5-3)^2+9=-4+9=5
\end{align*}
Note que o valor de y começa a repetir. Isto significa que o ponto \((3,9)\) é o vértice da parábola. Logo,
\begin{align*}
f(3) \amp =9\\
f(2) \amp =f(4)=8\\
f(1) \amp =f(5)=5\\
f(0) \amp =f(6)=0\\
f(-1) \amp =f(7)=-7\\
f(-2) \amp =f(8)=-16\\
f(-3) \amp =f(9)=-27
\end{align*}
Atividades
Seja a função quadrática
\(f(x)=3(x-2)^2\text{.}\) Analise os valores de y para
\(x\in\{-4,-3,-2,-1,0,1,2,3,4\}\text{,}\) mostrando quais são as coordenadas do vértice e quais são os valores de
\(x\) possuem os mesmos valores de
\(y\text{.}\) Solução.
Logo,
\begin{align*}
f(-4) \amp =3\cdot(-4-2)^2=3\cdot36=108\\
f(-3) \amp =3\cdot(-3-2)^2=3\cdot25=75\\
f(-2) \amp =3\cdot(-2-2)^2=3\cdot16=48\\
f(-1) \amp =3\cdot(-1-2)^2=3\cdot9=27\\
f(0) \amp =3\cdot(0-2)^2=3\cdot4=12\\
f(1) \amp =3\cdot(1-2)^2=3\cdot1=3\\
f(2) \amp =3\cdot(2-2)^2=3\cdot0=0\\
f(3) \amp =3\cdot(3-2)^2=3\cdot1=3\\
f(4) \amp =3\cdot(4-2)^2=3\cdot4=12
\end{align*}
Note que os valores de y começam a repetir a partir do ponto
\((2,0)\text{.}\) Isto significa que este ponto é o vértice da parábola. Logo,
\begin{align*}
f(2) \amp =0\\
f(1) \amp =f(3)=3\\
f(0) \amp =f(4)=12\\
f(-1) \amp =f(5)=27\\
f(-2) \amp =f(6)=48\\
f(-3) \amp =f(7)=75\\
f(-4) \amp =f(8)=108
\end{align*}
Seja a função quadrática
\(f(x)=-\dfrac{1}{2}(x-2)^2-3\text{.}\) Analise os valores de y para
\(x\in\{-6,-4,-2,0,2\}\text{,}\) mostrando quais são as coordenadas do vértice e quais são os valores de
\(x\) possuem os mesmos valores de
\(y\text{.}\) Solução.
\begin{align*}
f(-6) \amp =-\dfrac{1}{2}\cdot(-6+2)^2-3=-\dfrac{1}{2}\cdot(-4)^2-3=-\dfrac{1}{2}\cdot16-3=-8-3=-11\\
f(-4) \amp =-\dfrac{1}{2}\cdot(-4+2)^2-3=-\dfrac{1}{2}\cdot(-2)^2-3=-\dfrac{1}{2}\cdot4-3=-2-3=-5\\
f(-2) \amp =-\dfrac{1}{2}\cdot(-2+2)^2-3=-\dfrac{1}{2}\cdot(0)^2-3=-\dfrac{1}{2}\cdot0-3=-3\\
f(0) \amp =-\dfrac{1}{2}\cdot(0+2)^2-3=-\dfrac{1}{2}\cdot(2)^2-3=-\dfrac{1}{2}\cdot4-3=-2-3=-5\\
f(2) \amp =-\dfrac{1}{2}\cdot(2+2)^2-3=-\dfrac{1}{2}\cdot(4)^2-3=-\dfrac{1}{2}\cdot16-3=-8-3=-11
\end{align*}
Note que os valores de y começam a repetir a partir do ponto
\((-2,-3)\text{.}\) Isto significa que Este ponto é o vértice da parábola. Logo,
\begin{align*}
f(-2) \amp =-3\\
f(-4) \amp =f(0)=-5\\
f(-6) \amp =f(2)=-11
\end{align*}
Após analisar os pontos observados da função quadrática, encontrados segundo o cálculo de valor numérico, iremos inverter a análise dos resultados. E se for dado o valor de y, como encontramos o valor de x? Veremos alguns exemplos:
Dada a função quadrática \(f(x)=(x+1)^2-4\text{,}\) determine para qual valor de \(x\) temos \(f(x)=5\text{?}\)
Vamos solucionar o problema resolvendo a equação \((x+1)^2-4=5\text{.}\) Logo,
\begin{align*}
\amp (x+1)^2-4=5\\
\Rightarrow \amp (x+1)^2=5+4\\
\Rightarrow \amp (x+1)^2=9\\
\Rightarrow \amp x+1=\pm\sqrt9\\
\Rightarrow \amp x+1=\pm3
\end{align*}
Vamos abrir em duas duas possibilidades:
Assim, temos dois valores de x que determinam um \(f(x)=5\text{.}\) Ou seja, \(x=-4\) e \(x=2\text{.}\) Portanto, \(f(-4)=5\) e \(f(2)=5\text{.}\)
Exemplo 3.2.
Seja a função \(f(x)=-(x-3)^2+9\text{.}\) Determine x sabendo que \(f(x)=-16\text{.}\)
\begin{align*}
\amp -(x-3)^2+9=-16\\
\Rightarrow \amp (x-3)^2-9=16\\
\Rightarrow \amp (x-3)^2=16+9\\
\Rightarrow \amp (x-3)^2=25\\
\Rightarrow \amp x-3=\pm\sqrt25\\
\Rightarrow \amp x-3=\pm5
\end{align*}
Abrindo em dois casos temos que:
\begin{align*}
\amp x-3=5 \\
\Rightarrow \amp x=5+3 \\
\Rightarrow \amp x=8
\end{align*}
\begin{align*}
\amp x-3=-5\\
\Rightarrow \amp x=-5+3\\
\Rightarrow \amp x=-2
\end{align*}
Assim, temos dois valores de x que determinam um \(f(x)=5\text{.}\) Ou seja, \(x=-4\) e \(x=2\text{.}\) Portanto, \(f(-4)=5\) e \(f(2)=5\text{.}\)
Atividades
-
Seja a função \(f(x)=3(x-2)^2\text{.}\) Encontre o valor de x sabendo que f(x)=75.
Solução.
\begin{align*}
\amp 3(x-2)^2=75\\
\Rightarrow \amp (x-2)^2=\dfrac{75}{3}\\
\Rightarrow \amp (x-2)^2=25\\
\Rightarrow \amp x-2=\pm\sqrt25\\
\Rightarrow \amp x-2=\pm5
\end{align*}
Abrindo em dois casos:
\begin{align*}
\end{align*}
\begin{align*}
\amp x-2=5\\
\Rightarrow \amp x=5+2\\
\Rightarrow \amp x=7
\end{align*}
Assim, temos dois valores de x que determinam um \(f(x)=75\text{.}\) Ou seja, \(x=-3\) e \(x=7\text{.}\) Portanto, \(f(-3)=75\) e \(f(7)=75\text{.}\)
-
Dada a função \(f(x)=-\dfrac{1}{2}(x-2)^2-3\text{.}\) Determine x quando \(f(x)=-3\)
Solução.
\begin{align*}
\amp -\dfrac{1}{2}(x-2)^2-3=-3\\
\Rightarrow \amp -\dfrac{1}{2}(x-2)^2=-3+3\\
\Rightarrow \amp -\dfrac{1}{2}(x-2)^2=0\\
\Rightarrow \amp (x-2)^2=\dfrac{0}{-\dfrac{1}{2}}\\
\Rightarrow \amp (x-2)^2=0\\
\Rightarrow \amp x=\pm\sqrt0\\
\Rightarrow \amp x=0
\end{align*}
Assim, temos um valor de x que determina um \(f(x)=-3\text{.}\) Ou seja, \(x=0\text{.}\) Portanto, \(f(0)=-3\text{.}\)
Agora destacaremos alguns resultados específicos destes cálculos, onde a coordenada y dos pontos é igual a zero. Ou seja, daremos ênfase aos valores numéricos de que determinam y igual a zero, chamando assim esses valores de ZEROS DA FUNÇÃO QUADRÁTICA.
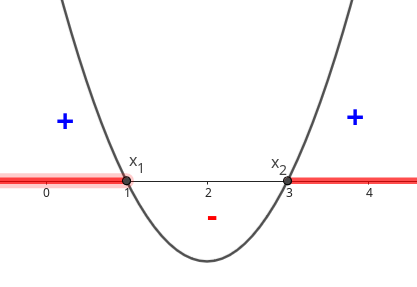
Por exemplo, na função quadrática \(f(x)=(x+1)^2-4\text{,}\) para \(x=-3\) e \(x=1\text{,}\) temos que \(f(-3)=0\) e \(f(1)=0\text{.}\) Ou seja, dizemos que -3 e 1 são os zeros da função quadrática.
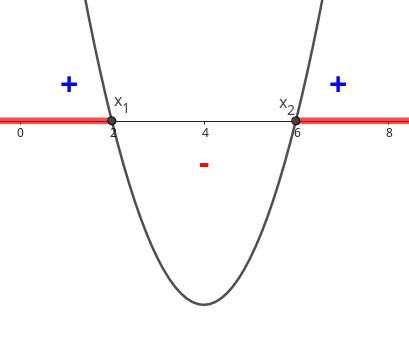
Analogamente, na função quadrática \(f(x)=-(x-3)^2+9\text{,}\) para \(x=0\) e \(x=6\text{,}\) temos que \(f(0)=0\) e \(f(6)=0\text{.}\) Logo, 0 e 6 são os zeros da função quadrática.
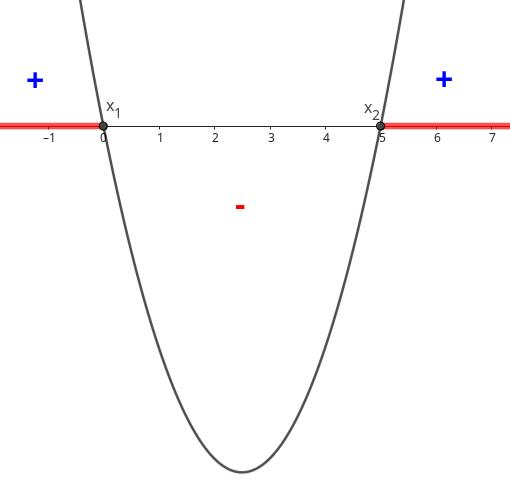
Da mesma forma, na função quadrática \(f(x)=3(x-2)^2\text{,}\) para \(x=2\text{,}\) temos que \(f(2)=0\text{.}\) Assim, 2 é o zero da função quadrática.
Por fim, na função quadrática \(f(x)=-\dfrac{1}{2}(x-2)^2-3\text{,}\) não é possível encontrar um valor de x tal que \(f(x)=0\text{.}\) Portanto, essa Função não têm zeros reais.